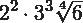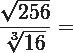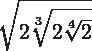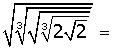Ejercicios de radicales con soluciones 3 ESO Descargar PDF

Bienvenido a este excelente artículo donde podrás aprender todos los conocimientos necesarios referentes a los radicales para que puedas conseguir ganarle la batalla a las matemáticas en el 3 ESO. Así que colócate en modo aprendizaje y conoce todo lo relacionado a este tema, al final del artículo podrás descargar un PDF con un completo solucionario y múltiples ejercicios.

Solucionario de Matematica Radicales 3 ESO Descargar en pdf

Se supone que si estás aquí es porque ya estas diestro con las raíces cuadradas y necesitas subir de nivel para llegar a los radicales o como comúnmente son conocidos “las raíces más complicadas”. Pero no te asustes que aquí aprenderás todo lo que necesitas.

¿Qué es un radical?

Con este nombre conseguimos definir a la operación de conseguir extraer las raíces de un número cualquiera. Aquí definitivamente debes de mantener la regla de que un radical es una expresión en donde la raíz n-enesima de “a” es igual a “b”, y “b” elevado a la “n” nos dará como resultado a “a”.

Evidentemente y como ha quedado demostrado con las anteriores palabras, la radicación es la operación opuesta a la potenciación. Debido a que si en una potencia somos capaces de multiplicar el mismo número varias veces; al calcular la raíz buscaremos un número que al multiplicarlo por sí mismo pueda darnos el número que tenemos dentro del radical.

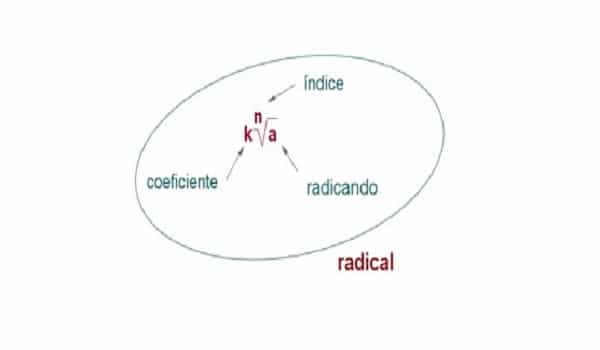
Partes de un radical

Mira un ejemplo práctico a continuación donde podrás notar y verificar cada una de las partes de un radical.

Potencias y radicales

Existe la posibilidad de conseguir expresar perfectamente un radical por medio de una potencia:

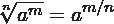
Veamos un ejemplo para una mejor ilustración:

Para ello colocaremos en forma de potencia al número 256, es decir 256 = $2^{8}$

Como puedes ver el índice del radical (2) será transformado en el denominador y colocaras al exponente del radicando (8) en el lugar del denominador; al efectuar las respectivas operaciones tendrás:

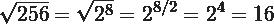
Resuelve algunos ejercicios:

$\sqrt{12} =$
$\sqrt{3} =$
$\sqrt[3]{4} =$
$\sqrt[5]{32} =$

Soluciones

$12 \tfrac{1}{2}$
$3\tfrac{1}{2}$
$4\tfrac{1}{3}$
$32\tfrac{1}{5}$

Radicales equivalentes

Por medo de la utilización de la notación del exponente fraccionario y por medio de la propiedad de las fracciones es posible afirmar que si multiplicas tanto el numerador como el denominador por un mismo número; la fracción resultante será una equivalente:

También es posible conseguir dicha equivalencia si procedes tato a multiplicar como a dividir tanto el índice como el exponente o exponentes del radicando por un mismo número (natural), aquí obtendrás un radical completamente equivalente.

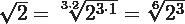
Resuelve algunos ejercicios:

$\sqrt[4]2{^{8}}$ (Multiplica por 3) =
$\sqrt[4]2{^{8}}$ (Dividimos entre 2) =

Soluciones

$\sqrt[12]2{^{24}}$
$\sqrt[]2{^{4}}$

Simplificación de radicales

Los radicales puedes simplificarlos y se consideran que ya están simplificados solo si no existe ningún tipo de signo de radical en el denominador, si por el contrario existiese algún signo radical en dicho denominador tendrás que racionalizar dicho denominador, ¿Cómo lo haces? Sencillísimo deberás de multiplicar el numerador y el denominador por el radical en el denominador.

Dicho de una manera más coloquial y sencilla, si consigues un número que divida tanto al índice así como al exponente (o a los exponentes en caso de haber varios) del radicando, esta evidentemente es la forma más sencilla de obtener un radical simplificado.

Veamos un ejemplo

Simplifiquemos $\sqrt[6]{256}$

Llevamos en forma de potencia al 256 y obtenemos 256 = $2^{8}$

Para conseguir la perfecta simplificación de este radical simplemente divides por 2 tanto al índice (6) como al propio exponente del radicando que en este caso es (8), con lo que obtienes:

$\sqrt[6]{256}$ = $\sqrt[6]2{^{8}}$ = $\sqrt[3]{2^{4}}$

Resuelve algunos ejercicios:

$\sqrt[]{8}$ =
$\sqrt[]{50}$ =
$\sqrt[3]{16}$ =
$\sqrt[]{54}$ =

Soluciones

$2\sqrt[]{2}$
$5\sqrt[]{2}$
$2\sqrt[3]{2}$
$3\sqrt[]{6}$

Reducción de un radical a índice común

El procedimiento para la reducción a común índice dos o más radicales es sumamente sencillo y simplemente tendrás que seguir las siguientes indicaciones.

Se procede a hallar el mínimo común múltiplo de cada uno de los índices, este obviamente será el índice común.
Luego procederás a dividir el común índice hallado entre cada uno de los índices y cada uno de los resultados obtenidos se multiplicara por los respectivos o correspondientes exponentes.

Veamos un ejemplo

Reduce los siguientes radicales:

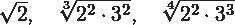
Para ello primeramente tendrás que colocar un índice común a cada uno de ellos. Para lo que tendrás que proceder a hallar el mínimo común múltiplo (m. c. m.) de los índices 2, 3 y 4 = este mínimo común múltiplo será (2, 3, 4) = 12.

Luego procedes a dividir este índice común (12) por cada uno de los índices correspondientes a cada radical (2, 3 y 4) y cada uno de estos resultados obtenidos lo multiplicaras por los respectivos o correspondientes exponentes.

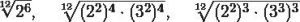
Luego llevas a cabo las operaciones con las potencias y logras obtener los resultados correspondientes a la reducción de cada uno de los radicales.

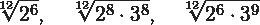
Resuelve algunos ejercicios:

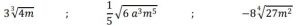
Soluciones

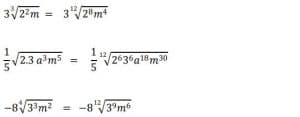
Extracción de los factores en un radical

Aquí es posible que puedan existir variantes, así que mucha atención a las explicaciones de este caso. Es de vital importancia tener claro que para conseguir extraer los factores de cualquier radical se deberá de descomponer el radicando en factores, pero solo si:

Algún exponente del radicando es menor que el propio índice; para este caso en particular dejas el factor correspondiente en el radicando; veamos un ejemplo:

$\sqrt[]{6} = \sqrt[]{2 . 3}$
$\sqrt[3]{9} = \sqrt[3]{3^{2}}$

Un exponente del radicando coincide en igualdad al índice; para este caso en particular deberás de sacar fuera del radicando al factor correspondiente; veamos un ejemplo:

$\sqrt[]{12} = \sqrt[]{2^{2}} . 3 = 2\sqrt[]{3}$

Como puedes notar debes de descomponer el número 12 en factores, pero como el 2 se encuentra elevado a la misma potencia que el índice entonces podrás extraer el 2 del radicando sin problemas.

2. $2\sqrt[3]{8} = \sqrt[3]{2^{3}} = 2$

Como puedes notar debes de descomponer el número 8 en factores, pero como el 2 se encuentra elevado a la misma potencia que el índice entonces podrás extraer el 2 del radicando.

Un exponente del radicando efectivamente es mayor que dicho índice, para este caso en particular deberás de dividir dicho exponente por el índice, luego el cociente que obtengas será el exponente del factor fuera del radicando y el resto pasara a convertirse en el exponente del factor dentro de dicho radicando. Veamos un ejemplo:

$\sqrt[]{48}$

Como el exponente del 2 es mayor que dicho índice, se deberá de dividir dicho exponente (4) entre el índice (2). Y obtendrás:

$\sqrt[]{48} = \sqrt[]{2^{4}} . 3 = 2^{2}\sqrt[]{3} = 4\sqrt[]{3}$

Como el cociente obtenido (2) es el exponente del factor que se encuentra fuera el radicando y el resto (0) será el factor que se encuentra dentro del radicando.

Además, el factor 20 fungiría como el exponente del factor fuera del radicando y el resto (0) sería el exponente del factor que se encuentra dentro del radicando.

Gracias a que el factor $2^{0}$ evidentemente es igual a 1, por lo que no necesitas de colocarlo en dicho radicando, ya que al multiplicarlo por otro factor este no tendría ningún tipo de variación. Por lo que tienes como regla general que si divides el exponente de un determinado actor por el índice y este arroja como resto cero, podrías obviar la colocación de ese factor en el radicando.

Resuelve algunos ejercicios:

$\sqrt[]{45} =$
$\sqrt[]{24} =$
$\sqrt[]{98} =$

soluciones

$3\sqrt[]{5}$
$2\sqrt[]{6}$
$7\sqrt[]{2}$

La introducción de factores en un radical

Para conseguir efectuar de manera satisfactoria este procedimiento deberás de elevar los factores al índice del radical. Como por ejemplo:

$a\sqrt[n]{b} = \sqrt[n]{a^{n}}b$

Veamos algunos ejemplos prácticos

$2\sqrt[]{3}$

Un ejemplo sencillo donde cómo puedes mirar el índice es 2, así como el factor fuera del radical es (2) y lo elevas al cuadrado, para proceder a realizar las operaciones correspondientes.

$2\sqrt[]{3} = \sqrt[]{2^{2}} . 3 = \sqrt[]{12}$

Otro ejemplo practico

Como pues notar, tanto el $2^{2}$ y el $3^{3}$ debes de introducirlos elevados a la cuarta potencia, de esta manera:

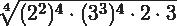
Luego procedes a eliminar los paréntesis, para lo que debes de multiplicar los exponentes

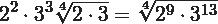
Y finalmente multiplicas las potencias que mantengan la misma base.

Resuelve algunos ejercicios:

$3\sqrt[]{2} =$
$4\sqrt[3]{2} =$
$2x\sqrt[3]{y} =$

Soluciones

$\sqrt[]{18}$
$\sqrt[3]{128}$
$\sqrt[3]{8x^{3}} y$

La suma de radicales

La suma de radicales también es una operación que podría destacarse como de suma sencillez, pero tienes que estar muy consciente que solo podrás sumarlos cuando estos sean radicales semejantes. O sea que mantengan el mismo índice y el mismo radicando.

Para las operaciones de resta se aplican los mismos principios que para la suma, igualmente para cuando quieras llevar a cabo combinaciones entre la suma y la resta.

Para llevar a cabo esta operación (donde mantienen el mismo índice y el mismo radicando) simplemente deberás de sumar los coeficientes de los radicales. Mira un ejemplo práctico.

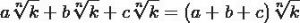
Resuelve algunos ejercicios:

$2\sqrt[]{2} - 4\sqrt[]{2} + \sqrt[]{2} =$
$3^{\sqrt[4]{5}} - 2\sqrt[4]{5} + \sqrt[4]{5} =$
$\sqrt[]{12} - 3\sqrt[]{3} + 2\sqrt[]{75} =$

Soluciones

$-\sqrt[]{2}$
O
$9\sqrt[]{3}$

La multiplicación de radicales

La multiplicación de radicales con el mismo índice

Para conseguir la efectiva multiplicación de radicales que mantengan el mismo índice deberás de multiplicar los radicandos al mismo tiempo que dejas el mismo índice. Mira un ejemplo práctico.

$\sqrt[n]{a} . \sqrt[n]{b} = \sqrt[n]{a . b}$

La multiplicación de radicales con diferente índice

Primeramente deberás de reducirlos a un común índice (explicación y ejercicios anteriormente explicados), luego si podrás proceder a efectuar la multiplicación. Mira un ejemplo práctico.

$\sqrt[]{3} . \sqrt[3]{9} . \sqrt[4]{27} =$

Efectivamente logramos la descomposición en factores de los radicandos.

$= \sqrt[]{3} . \sqrt[3]{3^{2}} . \sqrt[4]{3^{2}}$

Haces las reducciones a común índice para lo cual calculas el mínimo común múltiplo de cada uno de los índices, de la siguiente manera.

m. c. m. (2, 3, 4) = 12

Finalmente se divide el índice común (12) entre cada uno de los índices existentes (2, 3, 4) y a cada uno de estos resultados obtenidos se deberá de multiplicar por sus respectivos exponentes (1, 2, 3). Luego llevas a cabo la realización del producto de las potencias que mantengan la misma base en el radicando y se extraen los factores del radicando, para que la operación finalice de la siguiente manera.

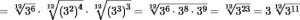
Resuelve algunos ejercicios:

$\sqrt[]{2} . \sqrt[]{6} =$
$\sqrt[]{7} . \sqrt[]{3} =$
$\sqrt[3]{2} . \sqrt[5]{16} =$
$3\sqrt[]{20} . 4\sqrt[]{18} =$

Soluciones

$2\sqrt[]{3}$
$\sqrt[]{21}$
$2\sqrt[15]{4}$
$72\sqrt[]{10}$

La división de radicales

La división de radicales con el mismo índice

Esta operación de división es sumamente semejante a la multiplicación y para conseguir efectuarla deberás de dividir los radicandos y por supuesto dejaras el mismo índice. Mira un ejemplo práctico.

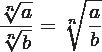
Resolvamos uno paso a paso para una mejor comprensión:

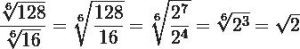
Como podrás verificar ambos radicales mantienen el mismo índice por lo que podrás colocarlo todo en un único radical con un mismo índice. Luego descompones en factores y procedes a llevar a cabo la división de potencias con una misma base. Seguidamente logras simplificar el radical efectuando la división entre el índice y el exponente el radicando por el número 3.

La división de radicales con diferente índice

Aquí la situación varia un poco ya que deberás de lograr conseguir la reducción a un índice común para luego proceder a llevar a cabo la división. Mira un ejemplo práctico.

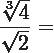
Como se logró explicar deberás de hacer la reducción a índice común, por esta razón deberás de calcular el mínimo común múltiplo (m. c. m.) de cada uno de los índices logrando conseguir que:

m. c. m. (3, 2) = 6

Seguidamente divides el índice común obtenido (6) entre cada uno de los índices (3 y 2) y a cada uno de los resultados conseguidos lo debes de multiplicar por su respectivo exponente (1 y 1).

Finalmente se descompone el 4 en factores para que puedas lograr efectuar la respectiva división de las potencias con una misma base y divides:

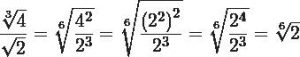
Resuelve algunos ejercicios:

$\frac{\sqrt[3]{24}}{\sqrt[3]{3}} =$

Soluciones

$4\sqrt[3]{4}$
2

Potencia de un radical

Si necesitas de elevar un radical a una potencia solo deberás de elevar a dicha potencia el radicando y por supuesto manteniendo el mismo índice. Mira un ejemplo práctico.

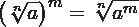
Otro ejemplo para una mejor comprensión

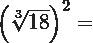
En este caso en particular deberás de elevar el radicando al cuadrado, luego descompones el número 18 en factores y seguidamente lo elevas al cuadrado, finalmente puedes extraer cada uno de los factores.

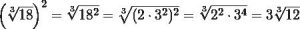
Resuelve algunos ejercicios:

$\left ( \sqrt[3]{18} \right )^{2} =$
$\left ( 2\sqrt[]{3} \right )^{2} =$
$\left ( 5\sqrt[]{7} \right )^{2} =$

Soluciones

$3\sqrt[3]{12}$
12
175

Raíz de un radical

De una manera sencilla y rápida la raíz de un radical no es más que otro radical con igualdad de radicando y que mantiene por índice al producto de los dos índices. Mira un ejemplo práctico.

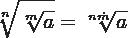
Resolvamos uno paso a paso para una mejor comprensión:

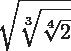
Procedes a la efectiva multiplicación de los indices

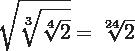
Resuelve algunos ejercicios:

Soluciones

$\sqrt[24]{2^{17}}$
$\sqrt[24]{2}$

Como has logrado verificar quiero que sepas que si has llegado hasta este punto es porque has efectuado un completo repaso de todo lo concerniente a radicación de 3 ESO, recuerda que puedes descargar para tus apuntes y practicas el solucionario con ejercidos en formato PDF con el cual tendrás acceso a conseguir un mejor dominio de la radicación. Si tienes algún comentario adicional así como si quieres contarnos algo sobre tu experiencia con esta actividad puedes dejarnos un comentario.

Indice y temas

¿Qué es un radical?
Partes de un radical
Potencias y radicales
Radicales equivalentes
Simplificación de radicales
Reducción de un radical a índice común
Extracción de los factores en un radical
La introducción de factores en un radical
La suma de radicales
La multiplicación de radicales
La división de radicales
Potencia de un radical
Raíz de un radical

Libro de soluciones de radicales 3 ESO en PDF

Haz click para abrir el PDF en versión online

ejercicios de radicales 3 ESO descargar PDF

Libros de Algebra
Calcular Matriz Inversa	MATRICES ¿ QUE ES UNA MATRIZ ?	tensores ejercicios resueltos
Determinante de una matriz 2×2	MÉTODO O REGLA DE CRAMER 3X3 2X2	tipos de matrices
Determinante de una matriz 3×3	Multiplicacion de matrices 2×2 3×3	Valores y vectores propios
Diagonalizacion de formas cuadraticas	Propiedades de los determinantes	Algebra Lineal
Espacio y subespacio vectorial	RANGO DE UNA MATRIZ	Algebra Lineal Sistemas
Matriz adjunta con ejercicios	SUMA DE MATRICES	Algebra Lineal y Geometria
matriz asociada a una metrica	Números enteros 1 ESO	Ejercicios de potencias y raíces 3 ESO
Ejercicios de radicales con soluciones 3 ESO