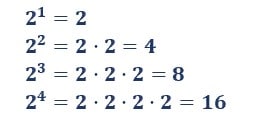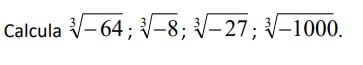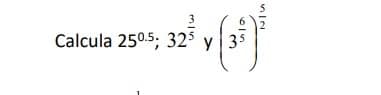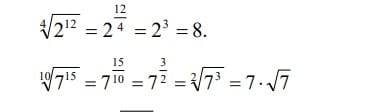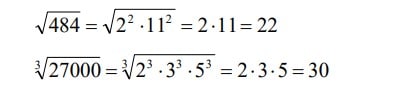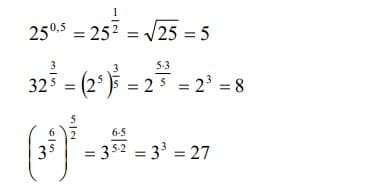Ejercicios de potencias y raíces 3 ESO Soluciones online y PDF

Bienvenido a este increíble post donde podrás comprender y repasar todo lo necesario referente a las potencias y a las raíces pertenecientes al curso 3 ESO, gracias a este solucionario podrás disponer de todas las diversas herramientas para conseguir poder enfrentar con todas las posibilidades de salir triunfante a las potencias y raíces de este año en específico. Así mismo te invito desde ya a lograr descargar el solucionario en formato PDF que se encuentra al final de este excelente artículo con infinidad de ejercicios y sus respectivas soluciones.

Solucionario de Potencias y Raíces 3 ESO Descargar en pdf

Cuando hablamos de potenciación hacemos referencia una operación matemática en la que existe un número denominado “base” el cual se multiplicara por sí mismo, tantas veces como lo indique otro número denominado “exponente”.

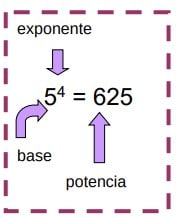
La potencia $a^{n}$ simplemente representa el producto que tiene (n) veces al número (a), así mismo el numero (a) se denomina base y el número (n) se denomina exponente.

Mira algunos ejemplos de potencias:

Operaciones con potencias 3 ESO

A continuación una breve explicación de cada una de las posibles operaciones con potencias (producto de potencias, cociente de potencias, potencia de un producto, potencia de un cociente y potencia de otra potencia) con una serie de ejercicios con sus respectivas soluciones para que logres ejercitarte al máximo con respecto a las potencias del curso 3 ESO.

Producto de potencias

Con la misma base

El resultado de un producto de potencias de la misma base siempre será otra potencia con dicha base (igual) y de exponente se colocara la suma de ambos exponentes.

Veamos un ejemplo para una mejor ilustración:

$b^{c}.b^{d}.b^{e} = b^{c+d+e}$

Resuelve algunos ejercicios:

$3^{4}.3^{2} =$
$z^{2}.z^{5}.z^{3} =$
$5^{3}.5^{4}.5^{2} =$

Soluciones

$3^{6}$
$z^{10}$
$5^{9}$

Con el mismo exponente

Para esta variante el resultado siempre será otra potencia que llevar una base que se calculara multiplicando las bases, obviamente elevadas al mismo exponente.

Veamos un ejemplo para una mejor ilustración:

$b^{a}.c^{a}.d^{a} = (b.c.d)^{a}$

Resuelve algunos ejercicios

Soluciones

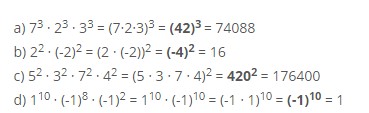
Cociente de potencias

Con la misma base

Para calcular de manera efectiva el cociente de potencias que mantengan la misma base se deberá de escribir otra potencia de igual base y como exponente se colocara el cálculo resultante de la resta de los exponentes anteriores.

Veamos un ejemplo para una mejor ilustración:

$b^{c} / b^{d} = b^{c-d}$

Resuelve algunos ejercicios

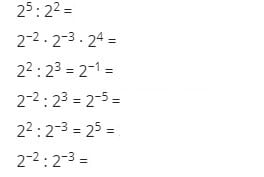
Soluciones

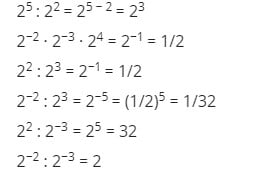
Con el mismo exponente

Para llevar a cabo una división de potencias con el mismo exponente se debe de dividir las bases y el resultado se deberá de elevar al mismo exponente.

Veamos un ejemplo para una mejor ilustración:

$a^{n} / b^{n} = (a/b)^{n}$

Resuelve algunos ejercicios

$18^{4} / 3^{4} =$

$(5)^{3} / (-14)^{3} =$

Soluciones

$(18/3)^{4} = 6^{4}$

$(5/-14)^{3}$

Potencias de exponente entero negativo

Para este cálculo se deberá de tener en cuenta que una potencia de base real $a\neq 0$ y de un exponente del tipo natural n < 0 siempre será el inverso e la misma con exponente positivo.

Veamos un ejemplo para una mejor ilustración:

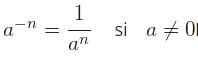
Resuelve algunos ejercicios

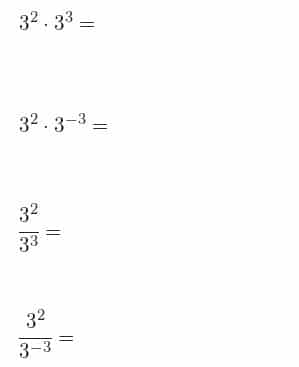
Soluciones

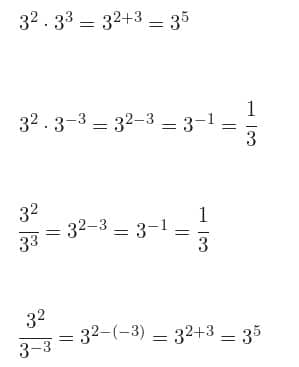
Potencia de un producto

Este cálculo puedes llevarlo a cabo de dos diferentes maneras:

Realizar el respectivo cálculo del producto y luego elevando dicho resultado a la respectiva potencia.
Elevar de manera individual cada uno de los factores a dicha potencia y finalizas realizando el respectivo producto.

Veamos un ejemplo para una mejor ilustración:

$(a.b.c.d)^{n} = a^{n}.b^{n}.c^{n}.d^{n}$

Resuelve algunos ejercicios

Soluciones

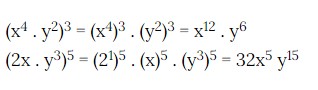
Potencia de un cociente

Este cálculo puedes llevarlo a cabo de dos diferentes maneras:

Realizar el respectivo cálculo del cociente y luego elevando dicho resultado a la respectiva potencia.
Elevar de manera individual el dividendo y el divisor a dicha potencia y finalizas efectuando dicho cociente.

Veamos un ejemplo para una mejor ilustración:

$(a/b)^{n} = a^{n} / b^{n}$

Resuelve algunos ejercicios

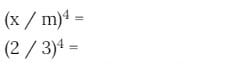
Soluciones

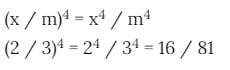
Potencia de otra potencia

Cuando llevas a cabo elevar una potencia a otra potencia entonces como resultado obtienes una potencia con la misma base y que llevara como exponente el producto resultante de dichos exponentes.

Veamos un ejemplo para una mejor ilustración:

$((d)^{m})^{n} = d^{m.n}$

Resuelve algunos ejercicios

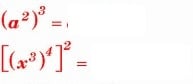
Soluciones

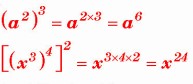
Potencias de números racionales

Para lograr conseguir la potencia de un número racional se deberá estar al tanto de que este resultado no es más que otro número racional cuyo numerador y denominador quedaran automáticamente elevados a dicha potencia.

Veamos un ejemplo para una mejor ilustración:

$(\frac{a}{b}) ^{n} = \frac{a^{n}}{b^{n}}$

Resuelve algunos ejercicios

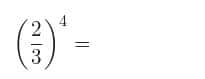
Soluciones

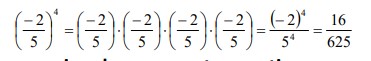
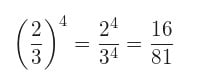
Potencia de base racional y exponente negativo

Cuando se eleva un número racional a una potencia negativa entonces el resultado es otra potencia pero donde llevara por base el mismo número racional pero inverso y elevado al mismo exponente pero ahora de signo positivo.

Veamos un ejemplo para una mejor ilustración:

$(\frac{a}{b}) ^{-n} = (\frac{b}{a}) ^{n} =$

Resuelve algunos ejercicios

$(\frac{3}{2}) ^{-4} =$

$(\frac{7}{9}) ^{-2} =$

Soluciones

$(\frac{3}{2}) ^{-4} = (\frac{2}{3}) ^{4} =$

$(\frac{7}{9}) ^{-2} = (\frac{9}{7}) ^{2} =$

Producto de potencias de base racional

Para estos cálculos se mantienen las propiedades de las potencias de base para los números naturales antes vistas.

Con la misma base

Aquí el resultado de multiplicar potencias de la misma base será una potencia con la misma base y por exponente se colocara la suma de dichos exponentes.

Veamos un ejemplo para una mejor ilustración:

$(a/b)^{c}.(a/b)^{d}.(a/b)^{e} = (a/b)^{c+d+e}$

Resuelve algunos ejercicios

$(2/3)^{5}.(2/3)^{2}.(2/3)^{4} =$

$(2/6)^{3}.(2/6)^{2}.(2/6)^{6} =$

Soluciones

$(2/3)^{5}.(2/3)^{2}.(2/3)^{4} = (2/3)^{5+2+4} = (2/3)^{11}$

$(2/6)^{3}.(2/6)^{2}.(2/6)^{6} = (2/6)^{3+2+6} = (2/6)^{11}$

Con el mismo exponente

Cuando multiplicas potencias con el mismo exponente el resultado será una potencia cuya base estará compuesta por el producto de dichas bases y estará elevada al mismo exponente.

Veamos un ejemplo para una mejor ilustración:

$(a/b)^{n}.(c/d)^{n}.(e/f)^{n} = [(\frac{a}{b}).(\frac{c}{d}).(\frac{e}{f})]^{n}$

Resuelve algunos ejercicios

$(1/2)^{3}.(5/6)^{3} =$

$(3/5)^{4}.(7/2)^{4} =$

Soluciones

$(1/2)^{3}.(5/6)^{3} = [(\frac{1}{2}).(\frac{5}{6})]^{3} = (\frac{6}{10})^{3}$

$(3/5)^{4}.(7/2)^{4} = [(\frac{3}{5}).(\frac{7}{2})]^{4} = (\frac{6}{35})^{4}$

Cociente de potencias de base racional

Con la misma base

Si divides potencias de una misma base racional obtendrás como resultado otra potencia con la misma base y cuyo exponente será el resultado de la diferencia de dichos exponentes.

Veamos un ejemplo para una mejor ilustración:

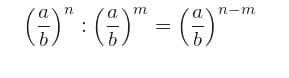
Resuelve algunos ejercicios

$(\frac{2}{3})^{5} : (\frac{2}{3})^{2} =$

$(\frac{5}{8})^{7} : (\frac{5}{8})^{2} =$

Soluciones

$(\frac{2}{3})^{5} : (\frac{2}{3})^{2} = (\frac{2}{3})^{5-2} = (\frac{2}{3})^{3}$

$(\frac{5}{8})^{7} : (\frac{5}{8})^{2} = (\frac{5}{8})^{7-2} = (\frac{5}{8})^{5}$

Con el mismo exponente

Cuando divides potencias con el mismo exponente tendrás como resultado una potencia cuya base es el cociente de dichas bases y estará elevada al mismo exponente.

Veamos un ejemplo para una mejor ilustración:

$(a/b)^{n}:(c/d)^{n} = [(\frac{a}{b}):(\frac{c}{d})]^{n}$

Resuelve algunos ejercicios

Soluciones

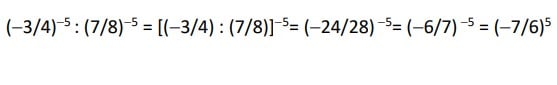
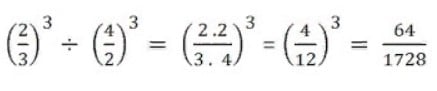
Operaciones con raíces 3 ESO

Radicales de índice cualquiera

Siempre se deberá de mantener el concepto de que la raíz enésima de un número “a” siempre será un número “x” que cuando lo elevas a “n” te da como resultado “a”.

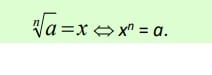
Es preciso recordar que:

n: es el índice de la raíz.

a: es el radicando

x: $\sqrt[n]{a}$ raíz

Potencias de exponente fraccionario

Siempre se define $x\tfrac{1}{n}$ como $\sqrt[n]{x}$

Es decir $x\tfrac{1}{n}$ $= \sqrt[n]{x}$

Por esta sencilla razón la potencia $x\tfrac{m}{n}$ puede perfectamente expresarse en forma de un perfecto radical, de esta forma “n” se establecerá como el índice de la raíz y “m” se establecerá como el exponente del radicando

De tal manera que $x\tfrac{m}{n}$ $= \sqrt[n]{x}^{m}$

Veamos un ejemplo para una mejor ilustración:

$5^{\frac{2}{3}}= \sqrt[3]{5}^{2}$

Resuelve algunos ejercicios

$7^{\frac{4}{2}}=$

$4^{\frac{6}{5}}=$

Soluciones

$7^{\frac{4}{2}}= \sqrt[]{7}^{4}$

$4^{\frac{6}{5}}= \sqrt[5]{4}^{6}$

Actividades con raíces de 3 ESO

Resuelve algunos ejercicios

Soluciones

Tomando en consideración que has logrado llegar al final de este estupendo post sobre las potencias y raíces de 3 ESO, es grata la oportunidad para invitarte nuevamente a descargar de manera gratuita el solucionario en formato PDF mediante el link que quiero dejarte a continuación, esta herramienta será perfecta para que puedas verificar lo aprendido en este post y lograr conseguir de manera efectiva el total dominio sobre la potenciación y la radicación del 3 ESO. Se te agradecería cualquier tipo de comentario a modo de expresarnos tu experiencia con este solucionario de ejercicios o alguna efectiva recomendación en pro de seguir mejorando en las próximas entregas.

Indice y temas

Producto de potencias
Cociente de potencias
Potencia de un producto
Potencia de un cociente
Potencia de otra potencia
Potencias de números racionales
Potencia de base racional y exponente negativo
Producto de potencias de base racional
Cociente de potencias de base racional
Operaciones con raíces 3 ESO
Radicales de índice cualquiera
Potencias de exponente fraccionario
Actividades con raíces de 3 ESO

Libro de soluciones de Potencias y Raíces 3 ESO en PDF

Haz click para abrir el PDF en versión online

Solucionario de potencias y raíces 3 ESO Soluciones onli

Libros de Algebra
Calcular Matriz Inversa	MATRICES ¿ QUE ES UNA MATRIZ ?	tensores ejercicios resueltos
Determinante de una matriz 2×2	MÉTODO O REGLA DE CRAMER 3X3 2X2	tipos de matrices
Determinante de una matriz 3×3	Multiplicacion de matrices 2×2 3×3	Valores y vectores propios
Diagonalizacion de formas cuadraticas	Propiedades de los determinantes	Algebra Lineal
Espacio y subespacio vectorial	RANGO DE UNA MATRIZ	Algebra Lineal Sistemas
Matriz adjunta con ejercicios	SUMA DE MATRICES	Algebra Lineal y Geometria
matriz asociada a una metrica	Números enteros 1 ESO	Ejercicios de potencias y raíces 3 ESO
Ejercicios de radicales con soluciones 3 ESO