Números enteros 1 ESO | Ejercicios y Soluciones PDF

Nada más importante para cualquier alumno actual que logran conocer los números enteros, después de los naturales estos son de suma importancia para los quehaceres diarios y para conseguir superar este escalón, a continuación un perfecto resumen sobre todo lo concerniente a los números enteros 1 ESO y desde donde podrás descargar un PDF con ejercicios y soluciones.

Solucionario Números enteros 1 ESO Descargar en pdf

Los números enteros, sus generalidades y sus definiciones

Los números positivos, negativos y el cero

Aquí puedes verificar que son tres diferentes significados y nada mejor que la representación gráfica de estos tres conceptos diferentes por medio de la recta numérica. Definitivamente los enteros positivos son lo que se encuentran a la derecha del cero (punto medio de la recta y sin valor) están precedidos en dicha recta por un signo “+”; el cero evidentemente al carecer de valor generalmente se puede escribir con cualquier signo o simplemente sin ninguno, y finalmente los negativos que se encuentran a la izquierda del cero en la recta numérica y que están precedidos de un signo “-“.

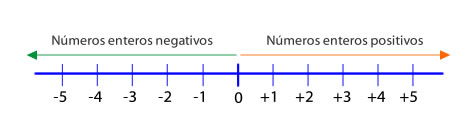
Es de destacar que tanto los números positivos, como los números negativos y por supuesto el cero; forman lo que denominamos como números enteros.

NOTA: hacia la derecha de la recta numérica los números aumentaran en valor, y hacia la izquierda de la recta numérica los números disminuirán de valor.

Enteros positivos: Se utilizan para representar el valor positivo de las cosas, altura, cantidad etc.
Enteros negativos: Se utilizan para determinar el valor negativo de las cosas, altura, deudas etc.
Cero: Punto neutro de la recta numérica y carece de valor.

El valor absoluto de un número entero

Este valor está determinado por la distancia que separa a este número del cero en la recta numérica y se debe de escribir entre dos barras | | y sin el signo que lo identifica. Ejemplos:

El valor absoluto de +6 será: |6|
El valor absoluto de -6 será: |6|

El opuesto de un número entero

Como su nombre lo indica este será otro número entero de igual valor absoluto pero de distinto signo. Ejemplos:

El opuesto de +6 será: -6
El opuesto de -6 será: +6

Ejercicios propuestos

Escribe a continuación el número que mejor represente cada una de las diferentes situaciones:

La temperatura hoy ha estado a 15 grados centígrados bajo cero: __________
Un águila puede volar a 100 metros de altura: __________
Actualmente no tengo ningún tipo de deuda: __________
Un submarino puede sumergirse a 200 metros de profundidad: __________
Mi coche está aparcado en el piso 3 del sótano: __________

Representa el valor absoluto de las siguientes cantidades:

153: __________
-14: __________
258: __________
-25: __________

Representa el opuesto de las siguientes cantidades:

Op (-5): __________
Op (12): __________
Op (-852): __________
Op (135): __________

Soluciones

Escribe a continuación el número que mejor represente cada una de las diferentes situaciones:

La temperatura hoy ha estado a 15 grados centígrados bajo cero: -15
Un águila puede volar a 100 metros de altura: 100
Actualmente no tengo ningún tipo de deuda: 0
Un submarino puede sumergirse a 200 metros de profundidad: -200
Mi coche está aparcado en el piso 3 del sótano: -3

Representa el valor absoluto de las siguientes cantidades:

153: |153|
-14: |14|
258: |258|
-25: |25|

Representa el opuesto de las siguientes cantidades:

Op (-5): 5
Op (12): -12
Op (-852): 852
Op (135): -135

La representación gráfica de los números enteros 1 ESO en la recta numérica

Esta representación es de suma importancia para conseguir la perfecta representación de un número entero en el plano espacial. Esta parte es de mucha importancia para conseguir y conocer el orden ideal en el conjunto de los números enteros.

Para representarlos debes de seguir los siguientes pasos:

Trazas una línea completamente horizontal y en el centro de la misma marcaras al cero.
Divides la recta en segmentos iguales de longitud 1, tanto a la izquierda como a la derecha del cero.
Colocas los números positivos 1, 2, 3… a la derecha del cero y en azul y los negativos -1, -2, -3… a la izquierda del cero en color rojo.

Mientras más a la derecha del cero este ubicado un número, mayor será este y mientras más a la izquierda del cero este ubicado un número, menor será su valor.

Ejemplo: Si miras la representación anterior de la recta numérica podrás afirma que el número 5 es mayor que el numero -8; además también podrás asegurar que el número 0 es mayor que el número -4.

Ejercicios propuestos

Realiza la recta numérica e identifica los siguientes números enteros:

-7, 0, +3, -5, 1, 8

Soluciones

Operaciones con números enteros

La suma de números enteros

La suma de los números enteros es una operación básica que es imprescindible de conocer para lograr un perfecto manejo y entendimiento de este tipo de números. Mira a continuación las posibles variables.

Suma de números enteros del mismo signo

En esta oportunidad la regla indica que se sumaran los valores absolutos de cada uno de los números (sumandos) y cuando obtengas dicho resultado le colocaras el signo en común. Mira un ejemplo práctico:

3 + 5 = 8, como ambos son positivos simplemente hallamos los valores absolutos de ambos números

+3= |3|

+5= |5|

Sumas estos dos valores absolutos: 3+5 = 8 y le colocas el signo común que es el positivo. Quedando de la manera: 3 + 5 = 8; Mira otro ejemplo con signo negativo:

(-3) + (-5) = -8

Igualmente al ser del mismo signo ambos números hallas el valor absoluto de ambos:

-3 = |3|

-5 = |5|

Sumas estos dos valores absolutos 3+5 = 8 y le colocas el signo común que es el negativo. Quedando de la manera 3 + 5 = -8.

Suma de números enteros de diferentes signo

Para llevar a cabo esta operación debes de tomar en consideración que los números positivos (+) suman mientras que los números (-) restan.

Para llevar a cabo esta operación nada mejor que apoyarte en la recta numérica, mira un ejemplo: halla la suma entre (+3) + (-7)=

Aquí fácilmente puedes comenzar desde el número “0” en la recta numérica y avanzar 3 espacios (+3) hacia la derecha y luego 7 pasos hacia la izquierda (-7); esto evidentemente te hará llegar hasta el (-4) que será el resultado de (+3) + (+7)= -4.

También puedes utilizar la siguiente regla: “para la obtención del resultado de la suma de dos números enteros de diferentes signo simplemente se restan sus valores absolutos; es decir al mayor le restas el menor y al resultado le colocas el signo del número de mayor valor absoluto. Mira un ejemplo práctico.

(- 2 ) + ( + 8 ) = 6

Hallas los dos valores absolutos: |2| y |8|, al mayor le restas el menor 8-2= 6; a este resultado le colocaras el signo del número con mayor valor absoluto que en este caso específico es el (+) del 8. Quedando (- 2 ) + ( + 8 ) = 6

Ejercicios propuestos

(-3)+5=
3+(-5)=
5+2=
(-5)+(-1)=

Soluciones

2
-2
7
-6

La resta de números enteros

Para llevar a cabo la resta de números enteros de una forma enteramente efectiva deberás de seguir la siguiente regla: deberás de sumar al minuendo el opuesto del sustraendo. Mira un ejemplo practico.

7 – 5 = donde efectivamente 7 es el minuendo y 5 el sustraendo, si al minuendo le sumas el opuesto del sustraendo la operación te resultara: 7 + (-5)= y aquí aplicas la norma de la suma de números enteros con signos diferentes que acabas de aprender en los ejercicios anteriores: ya sea apoyándote en la recta numérica o con el modo de valores absolutos el resultado de la operación será: 7 + (-5)= 2.

Ejercicios propuestos

15 – 4 =
(-3) – (+8) =
(-3) – (-8)=
8 – 11 =

Soluciones

11
11
5
-3

La combinación entre sumas y restas en los números enteros de 1 ESO

Para que puedas llevar a cabo exitosamente operaciones combinadas con números enteros es preciso que prestes la debida atención a las siguientes reglas o recomendaciones, ya que evidentemente puedes llegar a confundirte. Mira un ejemplo práctico.

(+2) + (-1) – (+3) – (-5) + (-8)

Primeramente deberás de:

Eliminar los paréntesis.
Llevar a cabo las adecuadas operaciones con los números resultantes.

Siempre manteniendo presente las siguientes reglas:

+ (+a) = +a
+ (-a) = -a
-(+a) = -a
-(-a) = +a

Al eliminar los respectivos paréntesis tendrás:

+ 2 – 1 – 3 + 5 – 8 =

7 – 12 = – 5

Ejercicios propuestos

(+8) – (+3) + (-2) =
(-7) + (-3) – (-5) =
(-4) – (-7) + (-5) – (-1) =
(-5) + (-6) – (-2) + (-3) =

Soluciones

+3
-5
-1
+12

Producto de los números enteros

Para que puedas conseguir correctamente multiplicar 2 números enteros es necesario que primeramente halles sus valores absolutos, y luego los multiplicaras normalmente, pero con la condición de seguir al pie de la letra las reglas de los signos:

“si ambos factores mantienen el mismo signo se asignara el símbolo (+) al resultado y si ambos factores mantienen diferentes signos entonces se asignara el signo (-) al resultado obtenido.

+ . + = +

– . – = +

+ . – = –

– . + = +

Mira un ejemplo práctico.

(+6) . (+4) = |6| . |4| = 24 y se colocara el signo (+) debido a la regla anteriormente descrita.

Ejercicios propuestos

(-3) . (-4) =
(+5) . (-3) =
(-7) . (+5) =
(8) . (3) =

Soluciones

División de los números enteros

Para que puedas conseguir correctamente dividir 2 números enteros es necesario que primeramente halles sus valores absolutos, y luego los dividas normalmente, pero con la condición de seguir al pie de la letra las reglas de los signos:

“si el dividendo y el divisor mantienen el mismo signo se asignara el símbolo (+) al resultado y si el dividendo y el divisor mantienen diferentes signos entonces se asignara el signo (-) al resultado obtenido.

+ / + = +

– / – = +

+ / – = –

– / + = +

Mira un ejemplo práctico.

(+20) / (+5) = |20| / |5| = 4 y se colocara el signo (+) debido a la regla anteriormente descrita.

Ejercicios propuestos

(+25) / (+5) =
(+16) / (-2) =
(+21) / (-3) =
(-36) / (+9) =

Soluciones

+5
+8
-7
-4

Potencias de los números enteros

Para que puedas conseguir calcular la potencia de cualquier número entero deberás de multiplicar la base de dicho número por si misma tantas veces como lo indique su exponente. Mira un ejemplo práctico.

$\left ( +2^{} \right )^{4} =$

= (+2) . (+2) . (+2) . (+2)

= + 16

Mira otro ejemplo

$\left ( -3^{} \right )^{3} =$

= (-3) . (-3) . (-3)

= – 27

Como puedes ver uno de los resultados es (+) de signo positivo mientras que otro es de signo (-) negativo, por lo que deberás de tener en consideración la siguiente regla:

Las potencias que mantienen una base negativa y un exponente par, siempre tendrán resultados positivos.
Las potencias que mantienen una base negativa y un exponente impar, siempre tendrán resultados negativos.

Ejercicios propuestos

$\left ( -2^{} \right )^{2} =$
$\left ( -2^{} \right )^{3} =$
$\left ( -5^{} \right )^{2} =$
$\left ( -5^{} \right )^{3} =$
$\left ( +3^{} \right )^{3} =$

Soluciones

+4
-8
+25
-125
+27

Jerarquía en las operaciones combinadas de números enteros 1 ESO

Debes de tener siempre claro ciertas reglas para conseguir que tus resultados sean perfectos en cuanto a la jerarquización de las operaciones con los números enteros. Así que trata de aprenderte de memoria la siguiente jerarquización de las operaciones:

Deberás de resolver primeramente las operaciones que se encuentren dentro de paréntesis.
Se realizan las operaciones de multiplicación así como de división en el orden estricto de izquierda a derecha.
Finalmente se realizan las operaciones de suma y resta.

Si has logrado llegar hasta el final de este post debes de haber adquirido los suficientes conocimientos en cuanto a los números enteros 1 ESO para lograr superar cualquier reto que tenga que ver con esta asignatura. Así mismo estarás en plena capacidad de conseguir resultados satisfactorios en cualquier tipo de operación con estos números enteros como por ejemplo (suma, resta, multiplicación, división y potenciación, así como con operaciones combinadas).

Quiero recomendarte que puedas descargar de manera gratis un PDF con el completo solucionario para que puedas practicar de manera Offline las veces que tú quieras y así conseguir una mejor practica en cuanto a los números enteros 1 ESO, así que espero tus comentarios o recomendación referentes a este espectacular material.

Resumen general de las operaciones con números enteros 1 ESO

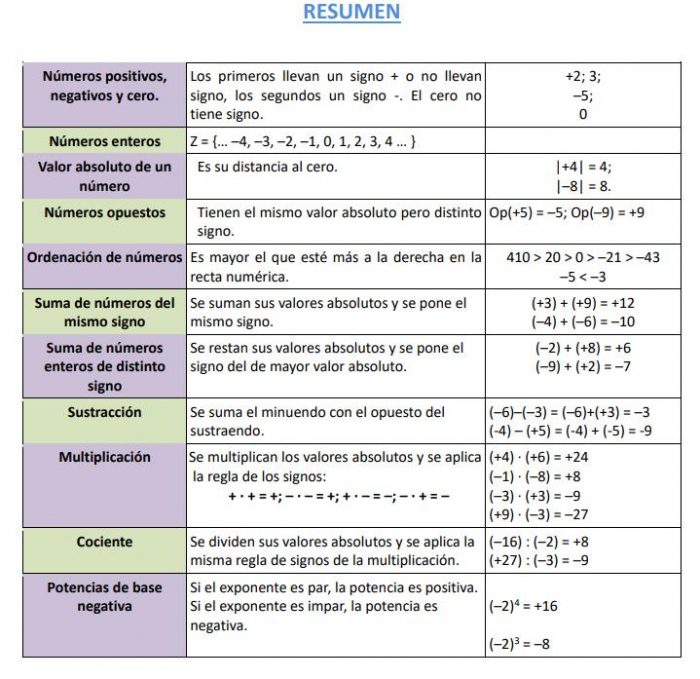
Indice y temas

Los números enteros, sus generalidades y sus definiciones
Los números positivos, negativos y el cero
El valor absoluto de un número entero
El opuesto de un número entero
La representación gráfica de los números enteros 1 ESO en la recta numérica
La suma de números enteros
La resta de números enteros
La combinación entre sumas y restas en los números enteros de 1 ESO
Producto de los números enteros
División de los números enteros
Potencias de los números enteros
Jerarquía en las operaciones combinadas de números enteros 1 ESO
Resumen general de las operaciones con números enteros 1 ESO

Libro de soluciones y ejercicios Números enteros 1 ESO

Haz click para abrir el PDF en versión online

Numeros enteros 1 ESO Ejercicios y Soluciones PDF

Libros de Algebra
Calcular Matriz Inversa	MATRICES ¿ QUE ES UNA MATRIZ ?	tensores ejercicios resueltos
Determinante de una matriz 2×2	MÉTODO O REGLA DE CRAMER 3X3 2X2	tipos de matrices
Determinante de una matriz 3×3	Multiplicacion de matrices 2×2 3×3	Valores y vectores propios
Diagonalizacion de formas cuadraticas	Propiedades de los determinantes	Algebra Lineal
Espacio y subespacio vectorial	RANGO DE UNA MATRIZ	Algebra Lineal Sistemas
Matriz adjunta con ejercicios	SUMA DE MATRICES	Algebra Lineal y Geometria
matriz asociada a una metrica	Números enteros 1 ESO	Ejercicios de potencias y raíces 3 ESO
Ejercicios de radicales con soluciones 3 ESO