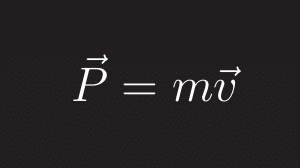Colisiones y choques física con ejercicios resueltos Mecanica

¿ Que son las colisiones y choques en física ? SIGNIFICADO y DEFINICIÓN

Se conoce como colisión o choque a una interacción breve entre varias partículas debido a una transferencia de momento y energía.

La interacción en las colisiones se considera como una fuerza interna y las fuerzas externas se pueden ignorar, considerando entonces un sistema aislado. Por lo tanto,  el momento lineal total se conserva en los choques o colisiones, es decir , el momento lineal total tendrá el mismo valor antes y después del choque.

Antes de continuar es necesario saber lo que es el momento lineal, pinchando aquí te lo explico.

Tipos de choques o colisiones

Dependiendo si se conserva o no la energía cinética encontramos:

• Choques elásticos: se conserva la energía cinética total
• Choques ineslasticos: no se conserva la energía cinética total.

Choques ELÁSTICOS / colisiones ELÁSTICAS

Como hemos visto, un choque es elásticos si cumple dos condiciones:

• Se conserva el momento lineal total
• Se conserva la energía cinética total

Estas dos condiciones se cumplen si las fuerzas que actúan entre los cuerpos que chocan son conservativas.

Formulas y ecuaciones de las colisiones ELÁSTICAS

Consideremos dos partículas de masa m_A y m_B , restringidos a moverse en una direccion , el eje x .

Llamamos  v_{A1} y  v_{B1} , las componentes de la velocidad antes del choque y  v_{A2} y  v_{B2} , las componentes de la velocidad después del choque.

Debido a la conservación del momento lineal:

m_Av_{A1}+m_Bv_{B1}=m_Av_{A2}+m_Bv_{B2}

Debido a la conservación de la energía cinética:

\dfrac{1}{2}m_Av_{A1}^2+\dfrac{1}{2}m_Bv_{B1}^2=\dfrac{1}{2}m_Av_{A2}^2+\dfrac{1}{2}m_Bv_{B2}^2

Estos son las ecuaciones a resolver en un choque elástico

Con un cuerpo inicialmente en reposo

Estudiaremos el caso de una colisión elástica con un cuerpo que esta inicialmente en reposo.

Para ello usamos las ecuaciones del choque elástico con la condición de  v_ {B1}=0 , es decir , el cuerpo B se encuentra en reposo.

Las ecuaciones quedan:

m_Av_{A1}=m_Av_{A2}+m_Bv_{B2}

\dfrac{1}{2}m_Av_{A1}^2=\dfrac{1}{2}m_Av_{A2}^2+\dfrac{1}{2}m_Bv_{B2}^2

Despejando y realizando calculos matematicos obtenemos:

m_Bv_{B2}^2=m_{A}(v_{A1}^2-v_{A2}^2)=m_{A}(v_{A1}-v_{A2})(v_{A1}+v_{A2})

m_Bv_{B2}^2=m_{A}(v_{A1}-v_{A2})

v_{B2}=v_{A1}+v_{A2}

m_{B}(v_{A1}+v_{A2})=m_{A}(v_{A1}-v_{A2})

Obteniendo las velocidades finales:

v_{A2}=\dfrac{m_A-m_B}{m_A+m_B}v_{A1}

v_{B2}=\dfrac{2m_A}{m_A+m_B}v_{A1}

Masas iguales

El caso de que las masas sean iguales, es decir, m_A=m_B=m, usando las ecuaciones de la velocidad obtenemos: v_{B2}=v_{A1} y v_{A2}=0.

Choque / colisión perfectamente INELASTICA

Una colisiona se denomina perfectamente inelastica si después de la colisión ambas partículas salen unidas con la misma velocidad final.

Formulas y ecuaciones de una colisión perfectamente inelastica

Como es un choque inelastico no se conserva le energía cinética y únicamente lo hace el momento lineal y teniendo en cuenta que v_{A2}=v_{B2}=v_F, obtenemos la ecuación de un choque perfectamente celestinesco

m_Av_{A1}+m_Bv_{B1}=(m_A+m_B)v_F

Con un cuerpo inicialmente en reposo

Si uno de los cuerpo esta en reposo , utilizando la ecuación anterior obtenemos:

v_{F}=\dfrac{m_A}{m_A+m_B}v_{A1}

Colisiones físicas y choques elasticas e inelasticas 10 EJEMPLOS Y EJERCICIOS RESUELTOS PASO A PASO

1. Sean dos partículas de m_A=5 \, kg y m_B=10 \, kg. La partícula B se encuentra en reposo y la partícula A choca elasticamente contra la B con una velocidad constante de v_A=15 \, \dfrac{m}{s}. ¿ Cuales son las velocidades finales de ambas partículas?

Como es un choque elástico se conserva le energía cinética y el momento lineal:

Debido a la conservación del momento lineal:

m_Av_{A1}+m_Bv_{B1}=m_Av_{A2}+m_Bv_{B2}

Debido a la conservación de la energía cinética:

\dfrac{1}{2}m_Av_{A1}^2+\dfrac{1}{2}m_Bv_{B1}^2=\dfrac{1}{2}m_Av_{A2}^2+\dfrac{1}{2}m_Bv_{B2}^2

Teniendo en cuenta que la particula B esta en reposo, es decir, v_{B1}=0 .

Despejamos de las ecuaciones de la conservación, las velocidades finales ,como hemos visto en la teoría, quedándonos:

v_{A2}=\dfrac{m_A-m_B}{m_A+m_B}v_{A1}

v_{B2}=\dfrac{2m_A}{m_A+m_B}v_{A1}

Sustituimos con nuestros datos del problema:

v_{A2}=\dfrac{5 \, kg-10 \, kg}{5 \, kg+10 \, kg}15 \, \dfrac{m}{s}=-5 \dfrac{m}{s}

v_{B2}=\dfrac{2 \cdot 5\, kg}{5 \, kg+10 \, kg}15 \, \dfrac{m}{s}=10 \dfrac{m}{s}

Aprende mas sobre Mecánica