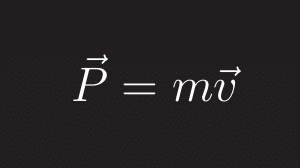¿ Que es el centro de masas en FÍSICA ? DEFINICIÓN
Denominamos centro de masas \vec{R}_{CM} del sistema al punto de coordenadas :
\vec{R}_{CM}=\dfrac{1}{M}\sum m_i\vec{r}_i
donde M=\sum m_i.
El centro de masas no tiene por que coincidir con ninguna particula del sistema.
Vector de posición del centro de masas
Formula del vector de posicion
El vector de posición del centro de masa es:
\vec{R}_{CM}=\dfrac{1}{M}\sum m_i\vec{r}_i
Formula del centro de masas con integrales
Si tenemos una distribución continua de masa podemos definir al centro de masas mediante integrales:
\vec{R}=\dfrac{1}{M}\int_V \vec{r}dm
Velocidad del centro de masas
Como ya sabemos , la velocidad es la derivada de la posición con respecto del tiempo.
Formula de la velocidad
Por lo tanto , podemos escribir la velocidad del centro de masas como:
\vec{V}_{CM}=\vec{\dot{R}}_{CM}=\dfrac{1}{M}\sum m \vec{\dot{r}}_i
Una vez conocida la velocidad , también podemos escribir el momento lineal o la cantidad de movimiento :
Formula del momento lineal
El momento lineal es:
\vec{P}_{CM}=M\vec{\dot{R}}_{CM}
Aceleración del centro de masas
Por ultimo vamos a ver la aceleración. La aceleración es la derivada temporal de la velocidad.
Formula de la ACELERACIÓN
Por lo tanto, para un centro de masas la aceleración es:
\vec{a}_{CM}=\vec{\ddot{R}}_{CM}=\dfrac{1}{M}\sum m \vec{\ddot{r}}_i
Como ya sabemos , la masa por la aceleración es una fuerza. Por lo tanto:
M \vec{a}_{CM}=\sum \vec{F}=\sum \vec{F}_{int}+\sum \vec{F}_{ext}
Por la tercera ley de Newton, todas las fuerza se cancelan en pares y el sumatorio de las fuerza internas se hace cero, quedando.
M \vec{a}_{CM}=\sum \vec{F}=\sum \vec{F}_{ext}
Este resultado es una demostración de que las fuerzas internas no afectan al movimiento del CM.
Por ultimo podemos relacionar la aceleración y la velocidad con las fuerzas externas y el momento lineal quedando:
\sum \vec{F}_{ext}=\dfrac{d\vec{P}}{dt}
Calculo del centro de masas ejercicios resueltos y ejemplos ( velocidad )
Sean tres cuerpos de masas 2 ,1 y 3 kg cuyos vectores de posicion son:
\vec{r_1}=5t\vec{i}-2t^2\vec{_j}+(3t-2)\vec{k};
\vec{r_2}=(2t-3)\vec{i}+(12-5t^2)\vec{j}+(4+6t-3t^3)\vec{k};
\vec{r_3}=(2t-1)\vec{i}+(2+t^2)\vec{j}+3t^3\vec{k};
Calcular
a) La velocidad del centro de masas en t=1
La velocidad del centro de masas es \vec{V}_{CM}=\vec{\dot{R}}_{CM}=\dfrac{1}{M}\sum m \vec{\dot{r}}_i. Por lo tanto, tenemos que calcular el vector de posicion del centro de masas y derivarlo respecto al tiempo.
Vector de posición del centro de masas \vec{R}_{CM}=\dfrac{1}{M}\sum m_i\vec{r}_i. Unicamente tenemos que sumar los vectores de posicion de cada particula quedando:
\vec{R}=(3t-2)\vec{i}+(3-t^2)\vec{j}+(2t-t^3)\vec{k}
Hacemos la derivada del este vector
\vec{\dot{R}}=3\vec{i}+(2t)\vec{j}+(2-3t^2)\vec{k}
Y sustituimos t=1, quedando
\vec{V}=\vec{\dot{R}}=3\vec{i}+(2)\vec{j}-\vec{k}
Ejercicios resueltos con integrales del centro de masas
Centro de masas de un triangulo rectangulo
Sea un triangulo rectángulo cuya ecuación es y=\dfrac{b}{a}x. Siendo b el cateto opuesto y a el cateto contiguo.
Primero calculamos la posición en x del centro de masas
x_{CM}=\dfrac{1}{M}\int xdm
Tenemos que calcular dm, para ello usamos la definición de densidad en superficie
dm=\sigma ydx=\dfrac{2M}{ab}ydx
Ahora
x_{CM}=\dfrac{1}{M}\int x\dfrac{2M}{ab}ydx
x_{CM}=\dfrac{2}{ab}\int_{0}^{a} xydx
Usando la ecuación de la recta para poner y en función de x obtenemos
x_{CM}=\dfrac{2}{ab}\int_{0}^{a}x\dfrac{bx}{a}dx=\dfrac{2}{3}a
En segundo lugar calculamos la posicion en y del centro de masas ( el procedimiento es igual pero en y)
y_{CM}=\dfrac{1}{M}\int ydm
dm=\sigma ydx=\dfrac{2M}{ab}ydx
y_{CM}=\dfrac{1}{M}\int x\dfrac{2M}{ab}ydx
Simplificando
y_{CM}=\int x\dfrac{y^2}{ab}dx
Sustituyendo y
y_{CM}=\dfrac{b^2}{a^2}\dfrac{1}{ab}\int_{0}^{a} x^rdx=\dfrac{b}{3}
Por lo tanto la posición del centro de masas queda:
\vec{r_{CM}}=\dfrac{2}{3}a\hat{x}+\dfrac{b}{3}a\hat{y}
Aprende sobre de MECÁNICA