Función logarítmica: definición, ejemplos, gráficas, ejercicios, dominio,etc.
Que es una función logarítmica Definición
Como concepto de función logarítmica podemos establecer:
Dado un numero cualquiera a tal que a>0 y a \neq 1 , definimos la función logarítmica en base a como la asociada a cada numero x>0 el unico valor, definido por log_{a}x , que cumple a^{log_a x}=x.
\log_a x=y\Leftrightarrow a^y=x
Funciones logarítmicas de base 10 se omite poner el 10 en la base y se pone directamentelog
Logaritmo neperiano o natural
El logartimo neperiano o natural , es aquel logaritmo cuya base es e
f(x)=Ln(x)
Función logarítmica ejemplos resueltos con gratifica
5 Ejemplos de funciones LOGARÍTMICAS
f(x)=\log(\dfrac{x-1}{x+2})
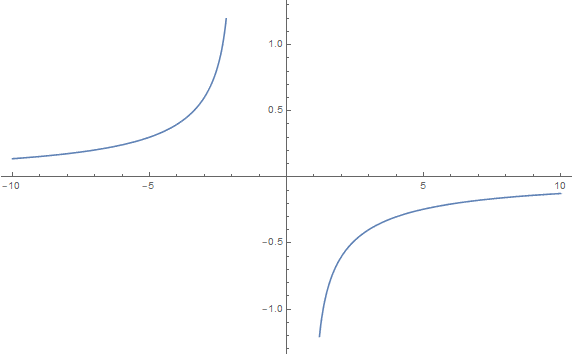
f(x)=\log(x^2+1)
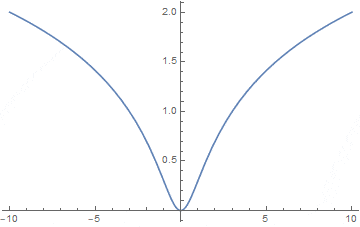
f(x)=\log(\dfrac{1}{x})
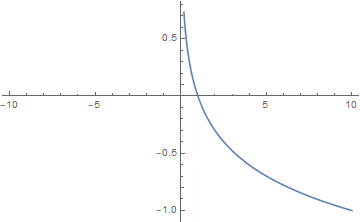
f(x)=\log(x^3)
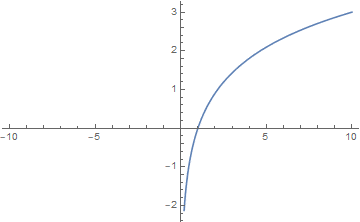
f(x)=\log(\sqrt{x^2+4})
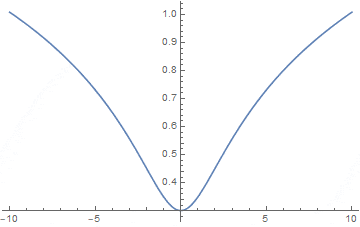
Como graficar una FUNCIÓN LOGARÍTMICA
Propiedades de la función logarítmica CARACTERÍSTICAS
Las propiedad o características de la función logaritmo son:
- Dominio de la función logarítmica (0,+ \infty ) .
- Recorrido \mathbb{R}
- La función logarítmica es continua
- La función logaritmo es creciente si a>1 y decreciente si a<1 .
- Es inyectiva
Dominio de la función logarítmica
El dominio de una función logaritmo tiene que estar definido para un numero mayor que cero . Demostración:
Si el dominio fuera menor o igual que cero, daría lugar a un a^y\leqslant 0 y esto es imposible debido a que a>0 .
Como log_a z= b\Leftrightarrow a^b=x y a>0 , por lo tanto x>0 .
Por lo tanto , el dominio de una función logarítmica es (0,+ \infty ) .
¿ Como hallar / sacar el dominio ?
Si tenemos una función logarítmica para hallar su dominio debemos restringir el dominio de la función que esta contenida en el logaritmo a (0,+ \infty).
f(x)=log_a g(x)
\mathrm{Dom}f(x)=\left \{ x \in \mathbb{R} / g(x)>0 \right \}
Ejemplos y ejercicio para sacar el dominio de una función logarítmica
- Obtén el dominio de la siguiente función f(x)=\log(\dfrac{x-1}{x+2})
Distinguimos las funciones f(x)\: g(x)
f(x) =\log(\dfrac{x-1}{x+2}) y g(x)=\dfrac{x-1}{x+2}
Por lo tanto el dominio de g(x)=\dfrac{x-1}{x+2} tiene que restringirse a mayor que cero, es decir, g(x)=\dfrac{x-1}{x+2} >0
El dominio de f(x)=g(x)=\dfrac{x-1}{x+2} es (-\infty , -2)\cap (1,+\infty)
Ejercicios resueltos paso a paso de funciona logarítmica
Ejercicio 1: Halla el dominio de la siguiente función
f(x)=\log (x^2-4)
Como el logaritmo esta definido solo para numero positivos:
\mathrm{Dom} f(x)=\left \{ x\in\mathbb{R}:x^2-1>0 \right \}=
=\left \{(-\infty,-2)\cup (2,+\infty) \right \}